3  Exploring Quantitative Data

3.1 Introduction

This is the first topic where we are going to see how to perform statistical analysis using two software: R and Python. Every language has it’s strengths and weaknesses, so instead of attempting to exactly replicate the same chart/output in each software, we shall try to understand their respective approaches better.

Our end goal is to analyse data - toward that end, we should be versatile and adaptable. Focus on learning how to be fast and productive in whichever environment you are told to work in. If you have a choice, then be aware of what each framework can do best, so that you can choose the right one.

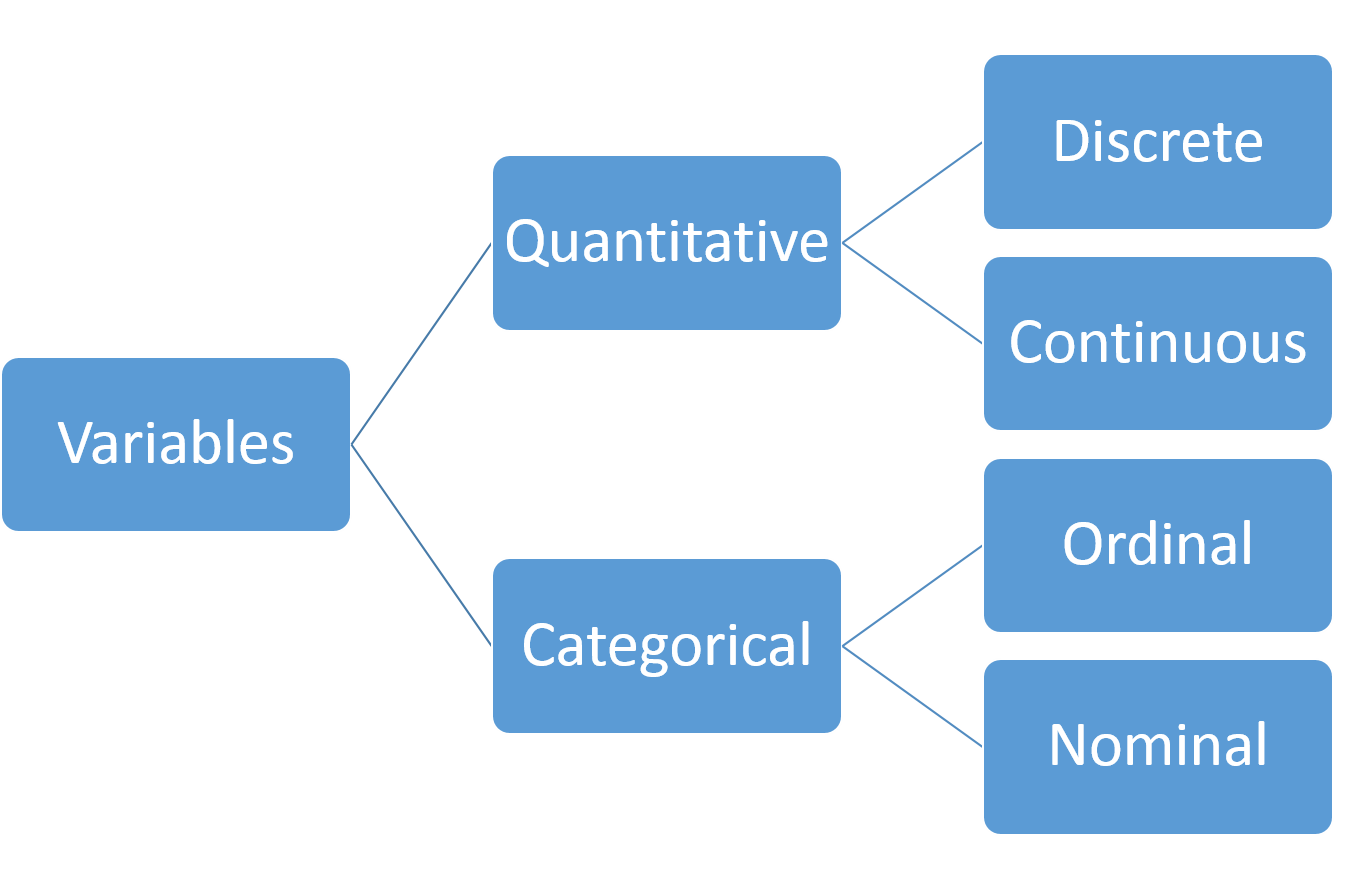
Although it is a simplistic view, the following diagram, Figure 3.1, provides a useful taxonomy of the types of columns we might have in our dataset. Having at least an initial inkling of the type of data matters, because it helps decide what type of summary to generate or what type of plot to make. Quantitative data are sometimes also referred to as numerical data.

Data types
Figure 3.1: Data types

There are two main ways of summarising data: numerically and graphically. This topic will cover:

  1. Numerical summaries for univariate quantitative variables.
  2. Numerical summary for association between two quantitative variables.
  3. Useful graphs for univariate and bivariate quantitative variables.

Techniques for categorical variables will be covered in Section 4.1.

Before proceeding, let us introduce one of the datasets that we’ll be using in this textbook. The dataset comes from the UCI Machine Learning Repository, which is a very useful place to get datasets for practice.

Example 3.1 (Student Performance: Dataset Introduction)

The particular dataset can be downloaded from this page. Once you unzip the file, you will find two csv files in the student/ folder:

  • student-mat.csv (performance in Mathematics)
  • student-por.csv (performance in Portugese)

Each dataset was collected using school reports and questionnaires. Each row corresponds to a student. The columns are attributes, including student grades, demographic information, and other social and school-related information. Each file corresponds to the students’ performance in one of the two subjects. For more information, you can refer to Cortez and Silva (2008).

# Feature Description (Type) Details
1 school student’s school (binary) “GP” - Gabriel Pereira, “MS” - Mousinho da Silveira
2 sex student’s sex (binary) “F” - female, “M” - male
3 age student’s age (numeric) from 15 to 22
4 address student’s home address type (binary) “U” - urban, “R” - rural
5 famsize family size (binary) “LE3” - less or equal to 3, “GT3” - greater than 3
6 Pstatus parent’s cohabitation status (binary) “T” - living together, “A” - apart
7 Medu mother’s education (numeric) 0 - none, 1 - primary education (4th grade), 2 - 5th to 9th grade, 3 - secondary education, 4 - higher education
8 Fedu father’s education (numeric) 0 - none, 1 - primary education (4th grade), 2 - 5th to 9th grade, 3 - secondary education, 4 - higher education
9 Mjob mother’s job (nominal) teacher, health, civil services, at_home, other
10 Fjob father’s job (nominal) teacher, health, civil services, at_home, other
11 reason reason to choose this school (nominal) close to home, school reputation, course preference, other
12 guardian student’s guardian (nominal) mother, father, other
13 traveltime home to school travel time (numeric) 1 - <15 min, 2 - 15 to 30 min, 3 - 30 min to 1 hour, 4 - >1 hour
14 studytime weekly study time (numeric) 1 - <2 hours, 2 - 2 to 5 hours, 3 - 5 to 10 hours, 4 - >10 hours
15 failures number of past class failures (numeric) n if 1<=n<3, else 4
16 schoolsup extra educational support (binary) yes or no
17 famsup family educational support (binary) yes or no
18 paid extra paid classes within the course subject (Math or Portuguese) (binary) yes or no
19 activities extra-curricular activities (binary) yes or no
20 nursery attended nursery school (binary) yes or no
21 higher wants to take higher education (binary) yes or no
22 internet Internet access at home (binary) yes or no
23 romantic with a romantic relationship (binary) yes or no
24 famrel quality of family relationships (numeric) from 1 - very bad to 5 - excellent
25 freetime free time after school (numeric) from 1 - very low to 5 - very high
26 goout going out with friends (numeric) from 1 - very low to 5 - very high
27 Dalc workday alcohol consumption (numeric) from 1 - very low to 5 - very high
28 Walc weekend alcohol consumption (numeric) from 1 - very low to 5 - very high
29 health current health status (numeric) from 1 - very bad to 5 - very good
30 absences number of school absences (numeric) from 0 to 93

In the explanatory variables above, notice that also severable variables have been stored in the dataset file using numbers, they are in fact categorical variables. Examples of these are variables 24 to 29. It seems fair to treat the three output columns as numeric though. G3 is the main output variable.

# Feature Description (Type) Details
31 G1 first period grade (numeric) from 0 to 20
32 G2 second period grade (numeric) from 0 to 20
33 G3 final grade (numeric, output target) from 0 to 20

3.2 Numerical Summaries

Numerical summaries include:

  1. Basic information about the data, e.g. number of observations and missing values.
  2. Measures of central tendency, e.g. mean, median
  3. Measures of spread, e.g. standard deviation, IQR (interquartile range), range.

Example 3.2 (Student Performance: Numerical Summaries)

Let us read in the dataset and generate numerical summaries of the output variable of interest (G3).

stud_perf <- read.table("data/student/student-mat.csv", sep=";", 
                        header=TRUE)
summary(stud_perf$G3)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.00    8.00   11.00   10.42   14.00   20.00 
sum(is.na(stud_perf$G3))
[1] 0
import pandas as pd
import numpy as np

stud_perf  = pd.read_csv("data/student/student-mat.csv", delimiter=";")
stud_perf.G3.describe()
count    395.000000
mean      10.415190
std        4.581443
min        0.000000
25%        8.000000
50%       11.000000
75%       14.000000
max       20.000000
Name: G3, dtype: float64
#stud_perf.G3.info()

From the output, we can understand that we have 395 observations, ranging from 0 to 20. I would surmise that the data is more or less symmetric in the middle (distance from 3rd-quartile to median is identical to distance from median to 1st-quartile). There are no missing values in the data.

However, summaries of a single variable are rarely useful since we do not have a basis for comparison. In this dataset, we are interested in how the grade varies with one or some of the other variables. Let’s begin with Mother’s education.

round(aggregate(G3 ~ Medu, data=stud_perf, FUN=summary), 2)
  Medu G3.Min. G3.1st Qu. G3.Median G3.Mean G3.3rd Qu. G3.Max.
1    0    9.00      12.00     15.00   13.00      15.00   15.00
2    1    0.00       7.50     10.00    8.68      11.00   16.00
3    2    0.00       8.00     11.00    9.73      13.00   19.00
4    3    0.00       8.00     10.00   10.30      13.00   19.00
5    4    0.00       9.50     12.00   11.76      15.00   20.00
table(stud_perf$Medu)

  0   1   2   3   4 
  3  59 103  99 131 
stud_perf[['Medu', 'G3']].groupby('Medu').describe()
         G3                                                  
      count       mean       std  min   25%   50%   75%   max
Medu                                                         
0       3.0  13.000000  3.464102  9.0  12.0  15.0  15.0  15.0
1      59.0   8.677966  4.364594  0.0   7.5  10.0  11.0  16.0
2     103.0   9.728155  4.636163  0.0   8.0  11.0  13.0  19.0
3      99.0  10.303030  4.623486  0.0   8.0  10.0  13.0  19.0
4     131.0  11.763359  4.267646  0.0   9.5  12.0  15.0  20.0

Now we begin to understand the context of G3 a little better. As the education level of the mother increases, the mean does increase. The middle 50-percent of the grade does seem to increase as well. The exception is the case where the mother has no education, but we can see that there are only 3 observations in that category so we should read too much into it.

Here are some things to note about numerical summaries:

  • If the mean and the median are close to each other, it indicates that the distribution of the data is close to symmetric.
  • The mean is sensitive outliers but the median is not. We shall see more about this in Section 5.1.
  • When the mean is much larger than the median, it suggests that there could be a few very large observations. It has resulted in a right-skewed distribution. Conversely, if the mean is much smaller than the median, we probably have a left-skewed distribution.

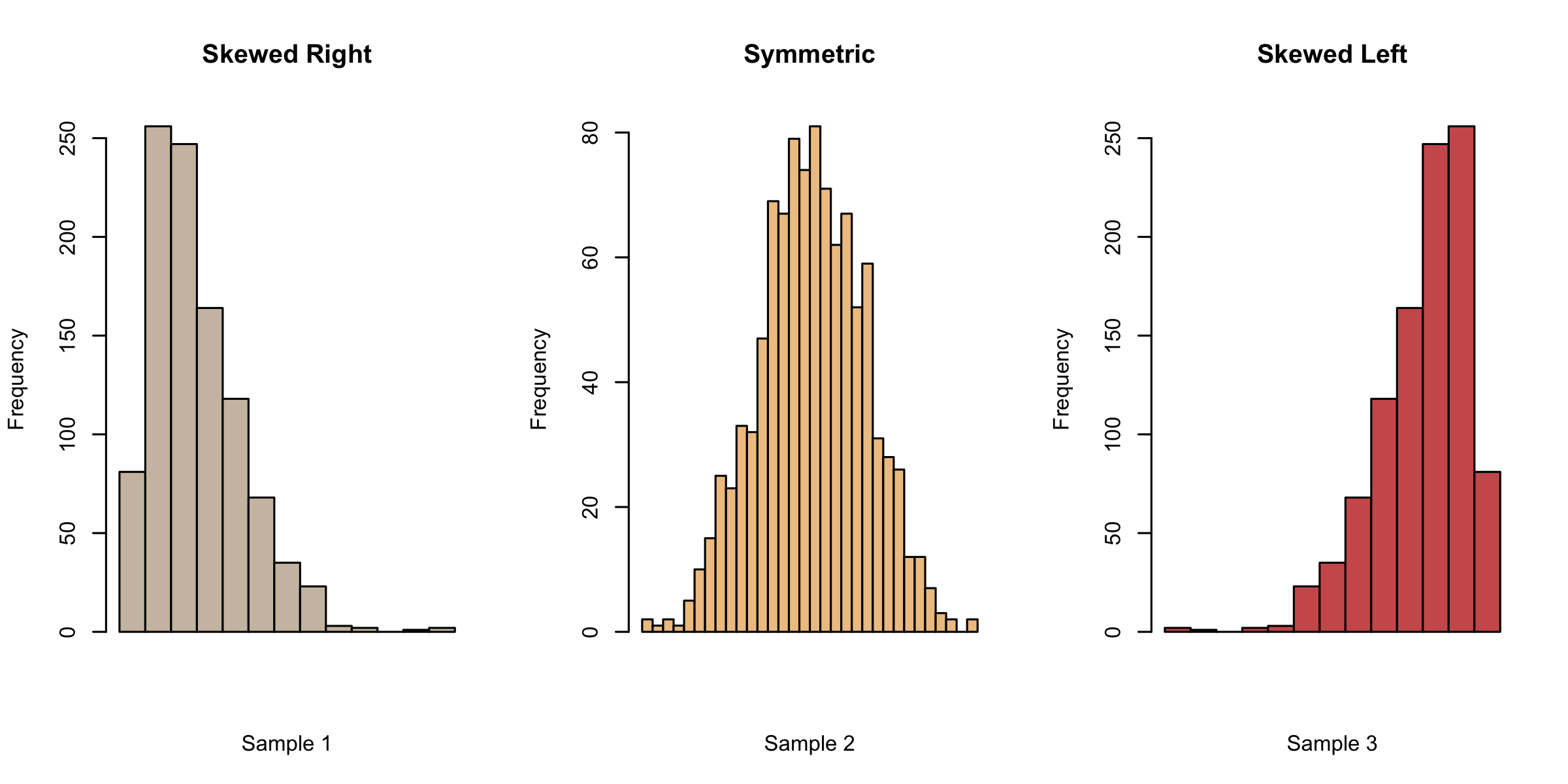
While numerical summaries provide us with some basic information about the data, they also leave out a lot. Even for experts, it is possible to have a wrong mental idea about the data from the numerical summaries alone. For instance, all three histograms in Figure 3.2 have a mean of 0 and standard deviation of 1!

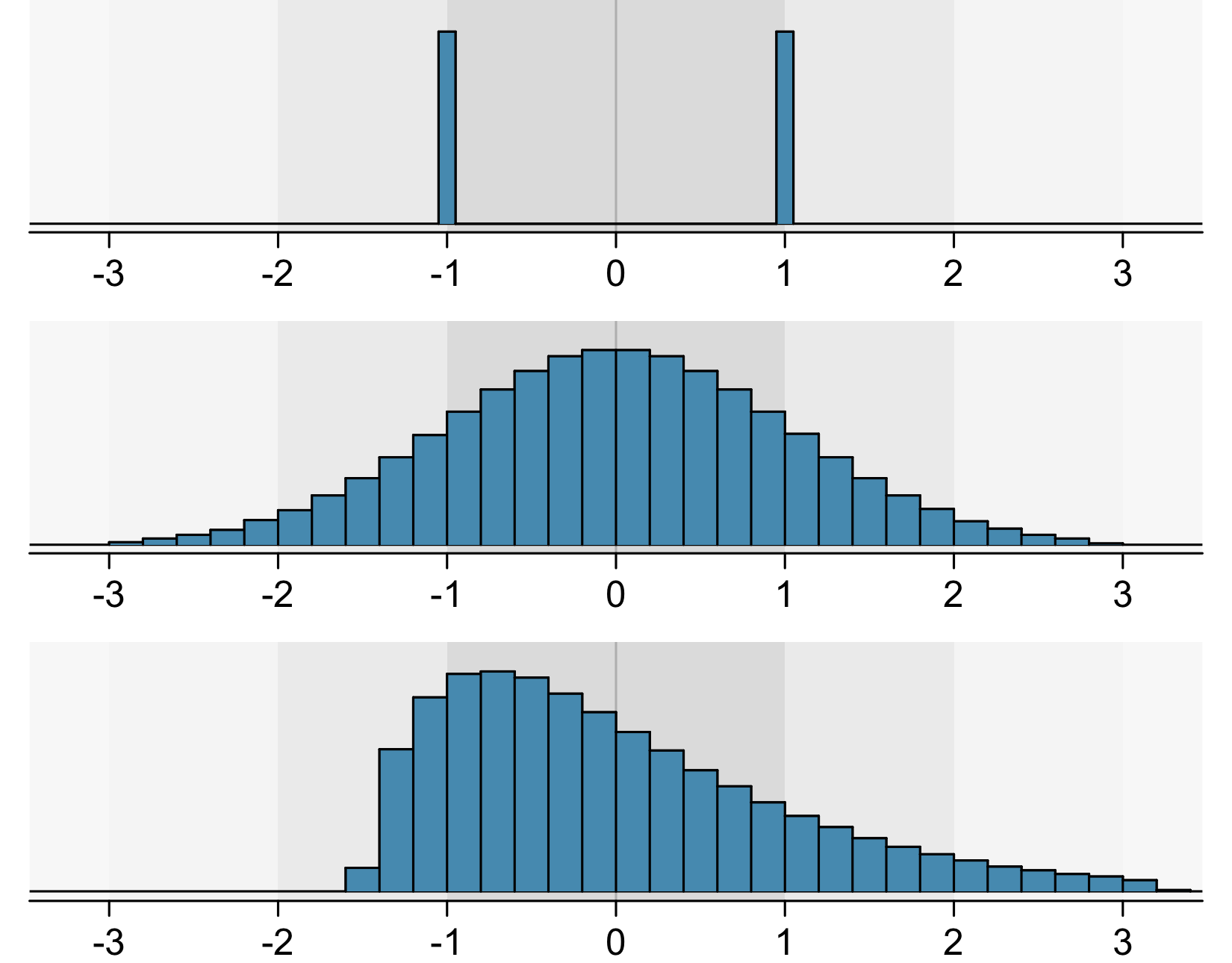
3 histograms
Figure 3.2: Three datasets with mean 0 and s.d. 1

That’s why we have to turn to graphics as well, in order to summarise our data.

3.3 Graphical Summaries

Histograms

The first chart type we shall consider is a histogram. A histogram is a graph that uses bars to portray the frequencies or relative frequencies of the possible outcomes for a quantitative variable.

When we create a histogram, here are some things that we look for:

  1. What is the overall pattern?: Do the data cluster together, or is there a gap such that one or more observations deviate from the rest?
  2. Do the data have a single mound or peak? If yes, then we have what is known as a unimodal distribution. Data with two ‘peaks’ are referred to as bimodal, and data with many peaks are referred to as multimodal. See Figure 3.4.
  3. Is the distribution symmetric or skewed? See Figure 3.5.
  4. Are there any suspected outliers? See Figure 3.3.
Figure 3.3: Histogram with outliers
Figure 3.4: Bimodal histogram
Figure 3.5: Skewed histograms

Example 3.3 (Student Performance: Histograms)

Now let us return to the student performance dataset.

hist(stud_perf$G3, main="G3 histogram")

fig = stud_perf.G3.hist(grid=False)
fig.set_title('G3 histogram');

Note

Do you notice anything different with the two histograms?

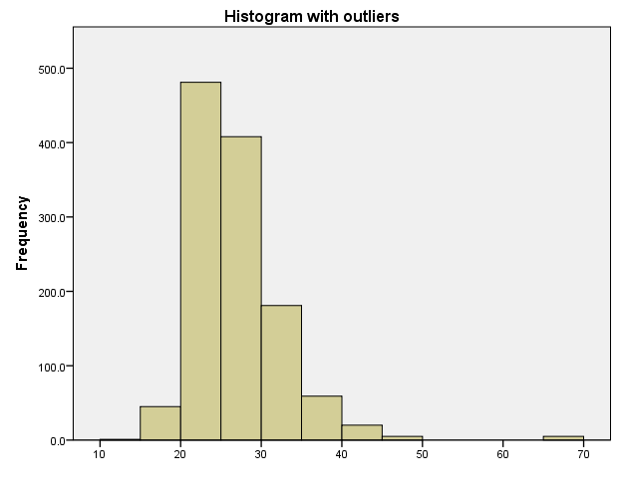
In general, we now have a little more information to accompany the 5 number summaries. It appears that the distribution is not a basic unimodal one. There is a large spike of about 40 students who scored very low scores.

As we mentioned earlier, it is not useful to inspect a histogram in a silo. Hence we shall condition on Mother’s education once more, to create separate histograms for each group. Remember that this is a case where the response variable G3 is quantitative, and the explanatory variable Medu is ordinal.

library(lattice)
histogram(~G3 | Medu, data=stud_perf, type="density",
          as.table=TRUE)

stud_perf.G3.hist(by=stud_perf.Medu, figsize=(15,10), density=True, 
                  layout=(2,3));

Although the heights of the panels in the two versions are not identical, we can, by looking at either one, see that the proportion of 0-scores reduces as the mother’s education increases. Perhaps this is reading too much into the dataset, but there seem to be more scores on the higher end for highest educated mothers.

Density Plots

Histograms are not perfect - when using them, we have to experiment with the bin size since this could mask details about the data. It is also easy to get distracted by the blockiness of histograms. An alternative to histograms is the kernel density plot. Essentially, this is obtained by smoothing the heights of the rectangles in a histogram.

Suppose we have observed an i.i.d sample \(x_1, x_2, \ldots, x_n\) from a continuous pdf \(f(\cdot)\). Then the kernel density estimate at \(x\) is given by

\[ \hat{f}(x) = \frac{1}{nh} \sum_{i=1}^n K \left( \frac{x - x_i}{h} \right) \] where

  • \(K\) is a density function. A typical choice is the standard normal. The kernel places greater weights on nearby points (to \(x\)).
  • \(h\) is a bandwidth, which determines which of the nearest points are used. The effect is similar to the number of bins in a histogram.

Example 3.4 (Student Performance: Density Estimates) 

densityplot(~G3, groups=Medu, data=stud_perf, auto.key = TRUE, bw=1.5)

import matplotlib.pyplot as plt
f, axs = plt.subplots(2, 3, squeeze=False, figsize=(15,6))
out2 = stud_perf.groupby("Medu")
for y,df0 in enumerate(out2):
    tmp = plt.subplot(2, 3, y+1)
    df0[1].G3.plot(kind='kde')
    tmp.set_title(df0[0])

As you can see, with density plots it is also possible to overlay them for closer comparison. This is not possible with histograms without some transparency in the rectangle colours.

Boxplots

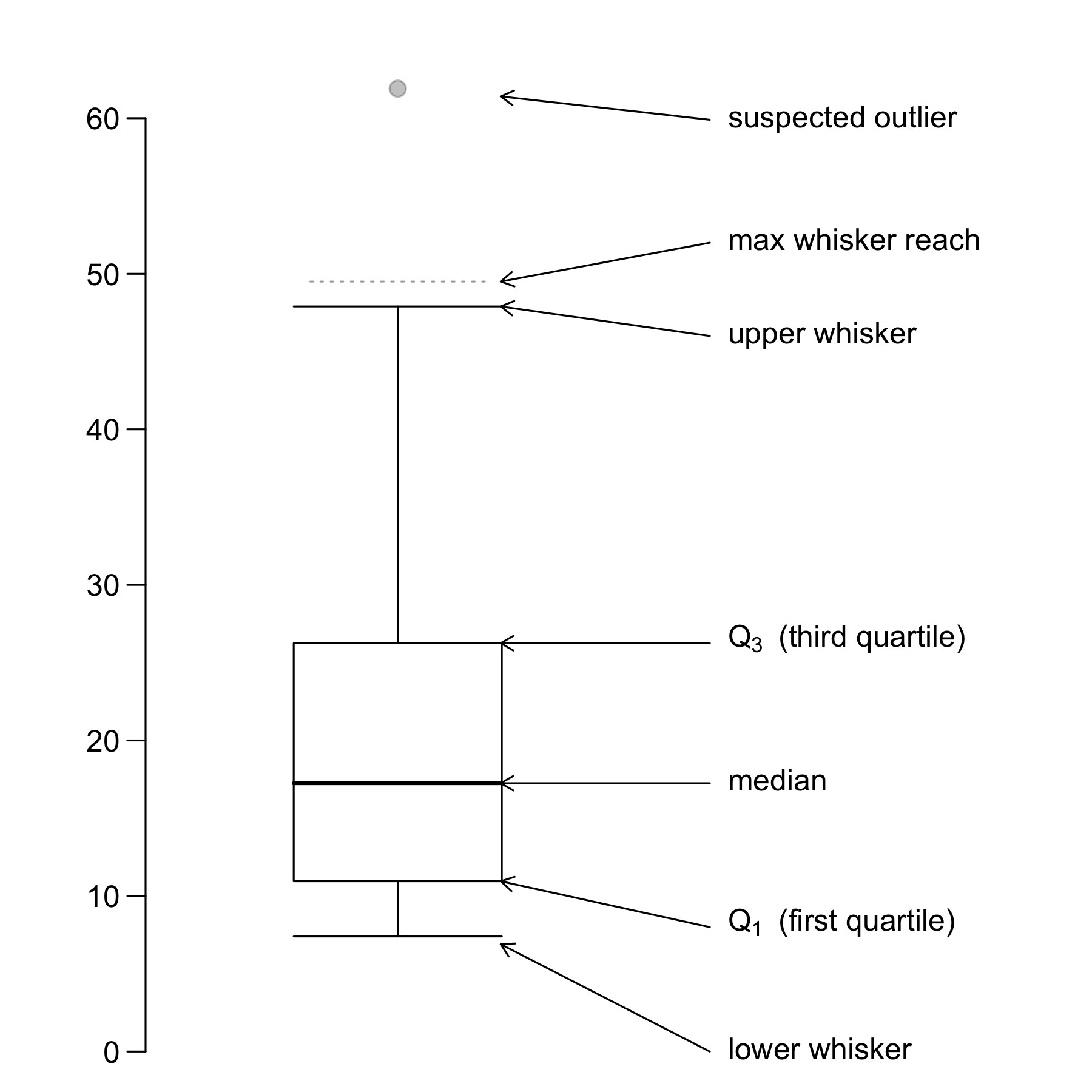
A boxplot provides a skeletal representation of a distribution. Boxplots are very well suited for comparing multiple groups.

Here are the steps for drawing a boxplot:

  1. Determine \(Q_1\), \(Q_2\) and \(Q_3\). The box is made from \(Q_1\) and \(Q_3\). The median is drawn as a line or a dot within the box.
  2. Determine the max-whisker reach: \(Q_3 + 1.5 \times IQR\); the min-whisker reach by \(Q_1 − 1.5 \times IQR\).
  3. Any data point that is out of the range from the min to max whisker reach is classified as a potential outlier.
  4. Excluding the potential outliers, the maximum point determines the upper whisker and the minimum point determines the lower whisker of a boxplot.

A boxplot helps us to identify the median, lower and upper quantiles and outlier(s) (see Figure 3.6).

Boxplot construction
Figure 3.6: Boxplot construction

Example 3.5 (Student Performance: Boxplots)

Instead of using mother’s education once again, we use the number of times a student goes out (goout) as the explanatory variable this time. From the boxplot outputs, it appears there is no strong strictly increasing/decreasing trend associated with G3. Instead, although the differences between the categories are not large, it seems as though there is an “optimal” number of times that students could go out. Too little and too much leads to lower median G3 scores.

bwplot(G3 ~ goout, horizontal = FALSE, data=stud_perf)

stud_perf.plot.box(column='G3', by='goout')
G3    Axes(0.125,0.11;0.775x0.77)
dtype: object

QQ-plots

Finally, we turn to QQ-plots. A Quantile-Quantile plot is a graphical diagnostic tool for assessing if a dataset follows a particular distribution. Most of the time we would be interested in comparing against a Normal distribution.

A QQ-plot plots the standardized sample quantiles against the theoretical quantiles of a N(0; 1) distribution. If they fall on a straight line, then we would say that there is evidence that the data came from a normal distribution.

Especially for unimodal datasets, the points in the middle will typically fall close to the line. The value of a QQ-plot is in judging if the tails of the data are fatter or thinner than the tails of the Normal.

(a) Thinner than Normal
(b) Fatter than Normal
Figure 3.7: QQ-plots
Note

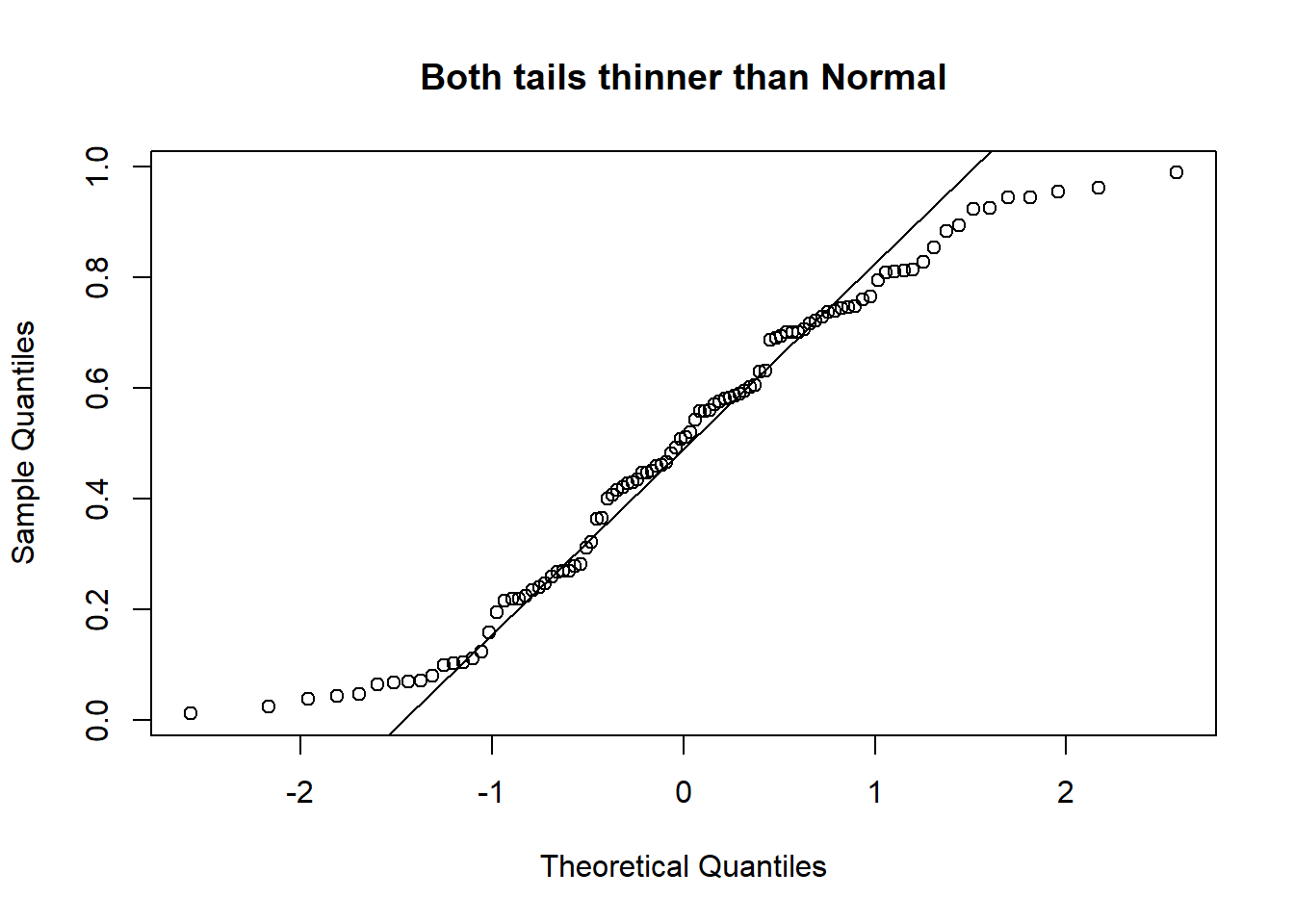
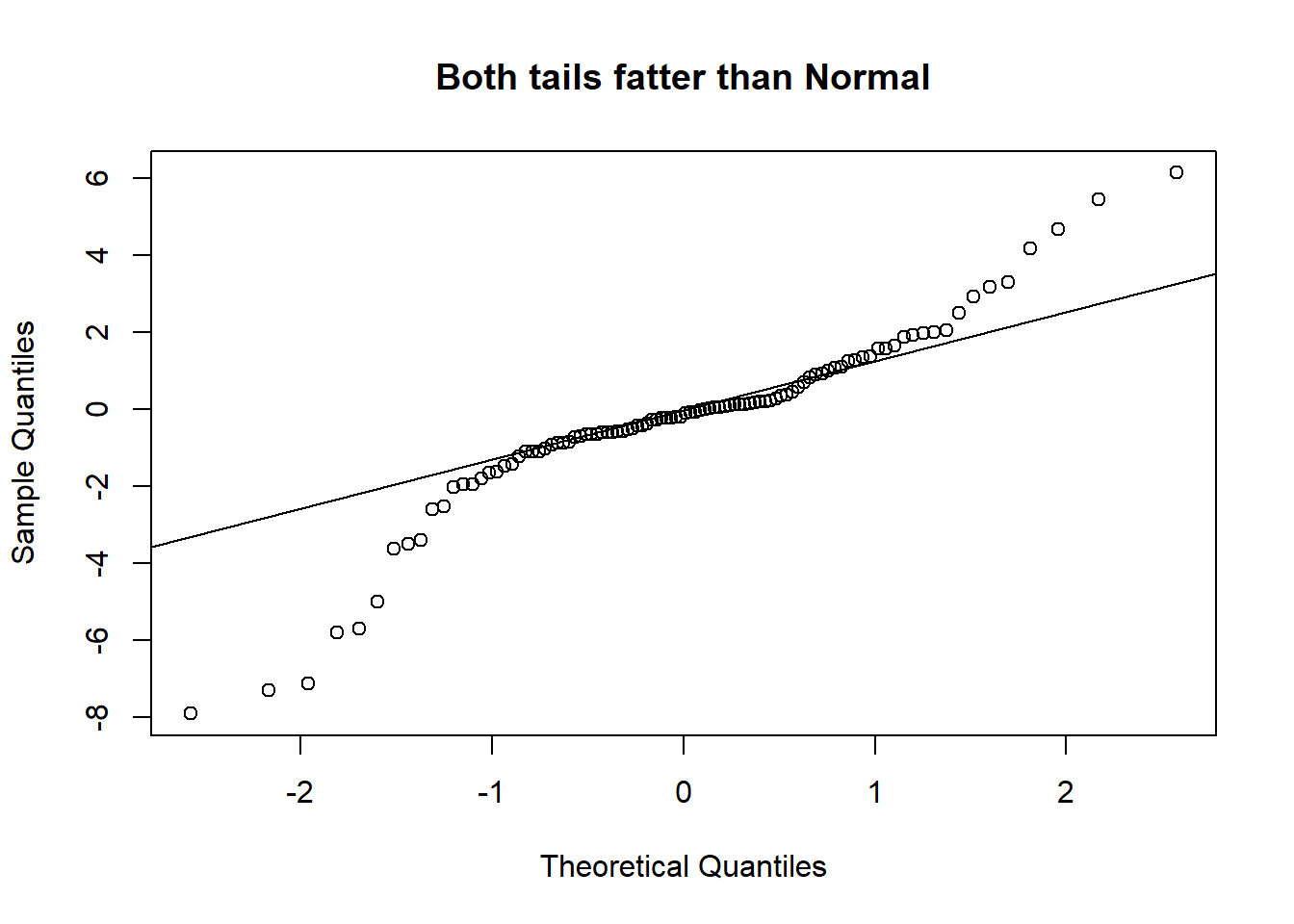
Please be careful! Some software/packages will switch the axes (i.e. plot the sample quantiles on the x-axis instead of the y-axis, unlike Figure 3.7). Please observe and interpret accordingly.

Example 3.6 (Concrete Slump: Dataset Introduction)

Concrete is a highly complex material. The slump flow of concrete is not only determined by the water content, but that is also influenced by other concrete ingredients. The UCI page for this dataset is here. The reference for this article is Yeh (2007).

The data set includes 103 data points. There are 7 input variables, and 3 output variables in the data set. These are the input columns in the data, all in units of kg per \(m^3\) concrete:

# Feature Details
1 Cement
2 Slag
3 Fly ash
4 Water
5 SP A super plasticizer to improve consistency.
6 Coarse Aggr.
7 Fine Aggr.

There are three output variables in the dataset. You can read more about Slump and Flow from this wikipedia page.

# Feature Units
1 SLUMP cm
2 FLOW cm
3 28-day Compressive Strength MPa

To read in the data in R:

concrete <- read.csv("data/concrete+slump+test/slump_test.data")
names(concrete)[c(1,11)] <- c("id", "Comp.Strength")
concrete = pd.read_csv("data/concrete+slump+test/slump_test.data")
concrete.rename(columns={'No':'id', 
                         'Compressive Strength (28-day)(Mpa)':'Comp_Strength'},  
                inplace=True)

Let us consider the Comp.Strength output variable. The histogram overlay in Figure 3.8 suggests some skewness and fatter tails than the Normal.

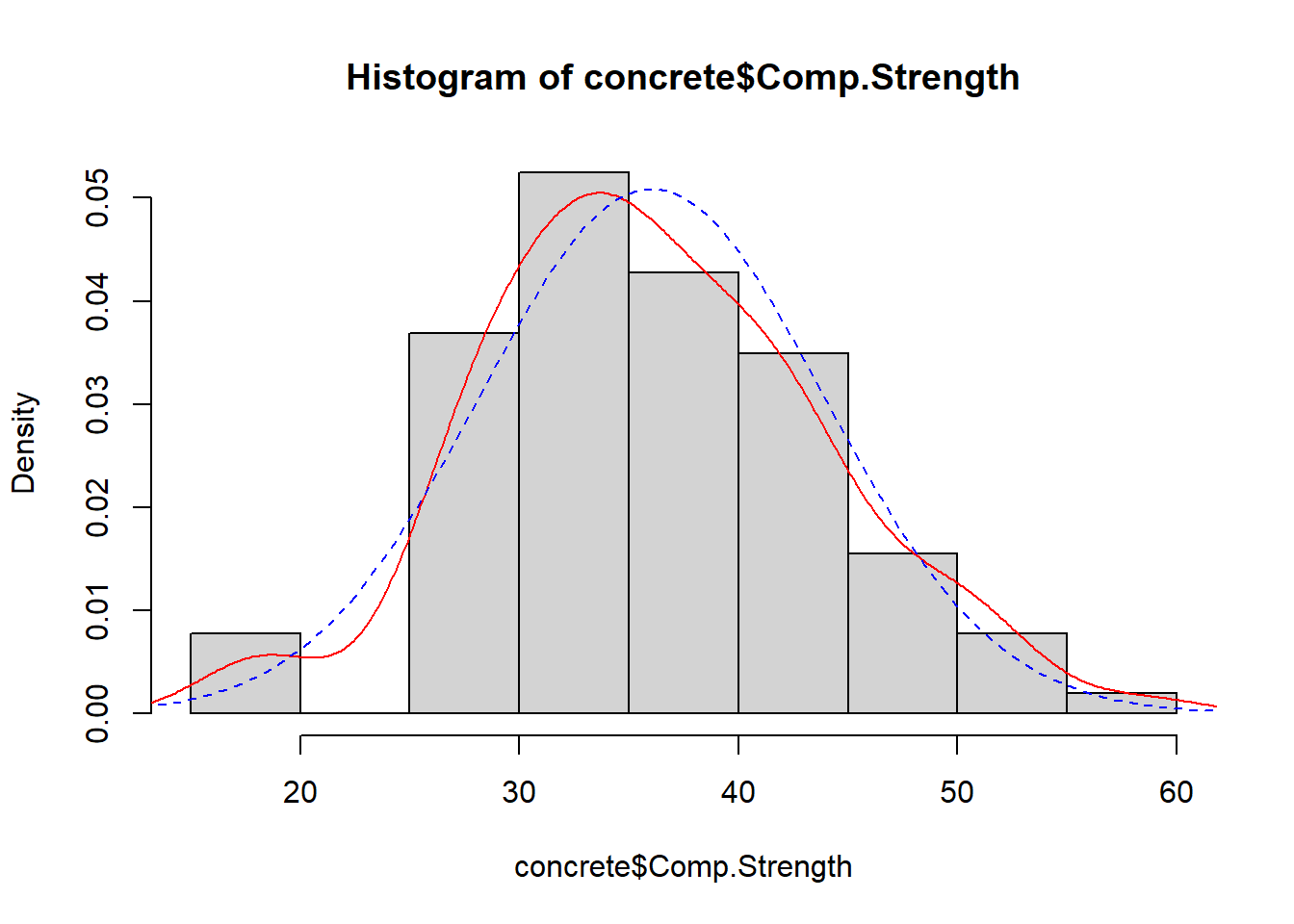
Figure 3.8: Comparing data with reference Normal (blue)

Example 3.7 (Concrete: QQ-plots)

The next chart is a QQ-plot, for assessing deviations from Normality.

qqnorm(concrete$Comp.Strength)
qqline(concrete$Comp.Strength)

from scipy import stats
import statsmodels.api as sm
sm.qqplot(concrete.Comp_Strength, line="q");

The deviation of the tails does not seem to be that large, judging from the QQ-plot.

3.4 Correlation

When we are studying two quantitative variables, the most common numerical summary to quantify the relationship between them is the correlation coefficient. Suppose that \(x_1, x_2, \ldots, x_n\) and \(y_1, \ldots, y_n\) are two variables from a set of \(n\) objects or people. The sample correlation between these two variables is computed as:

\[ r = \frac{1}{n-1} \sum_{i=1}^n \frac{(x_i - \bar{x})(y_i - \bar{y})}{s_x s_y} \] where \(s_x\) and \(s_y\) are the sample standard deviations. \(r\) is an estimate of the correlation between random variables \(X\) and \(Y\).

Figure 3.9: Linear Relation
Figure 3.10: Non-linear relation

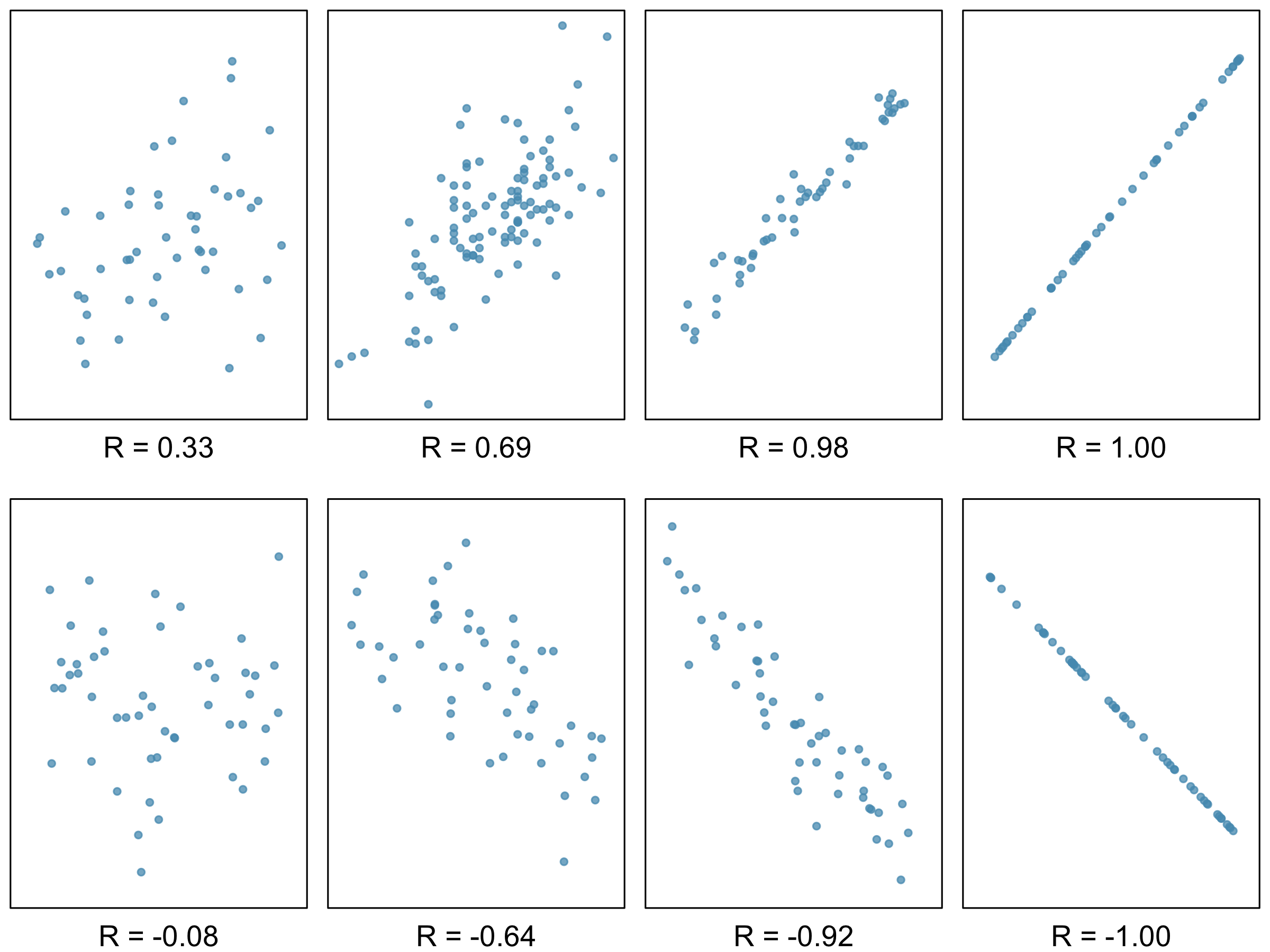
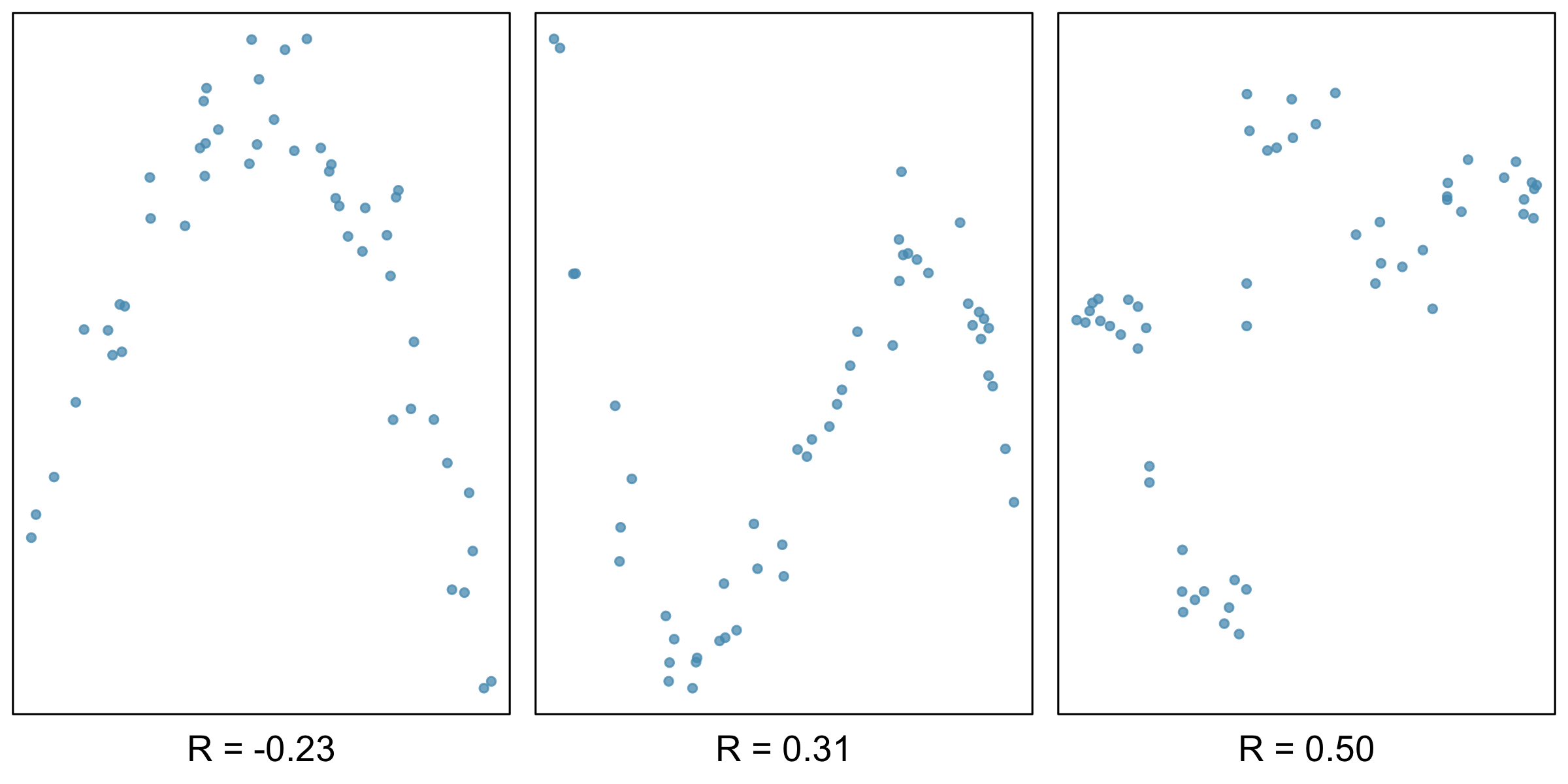
A few things to note about the value \(r\), which is also referred to as the Pearson correlation:

  • \(r\) is always between -1 and 1.
  • A positive value for \(r\) indicates a positive association and a negative value for \(r\) indicates a negative association.
  • Two variables have the same correlation, no matter which one is coded as \(X\) and which one is coded as \(Y\).

Figure 3.9 and Figure 3.10 contain sample plots of data and their corresponding \(r\) values. Notice how \(r\) does not reflect strong non-linear relationships.

3.5 Scatterplot Matrices

Example 3.8 (Concrete: Scatterplots) When we have multiple quantitative variables in a dataset, it is common to create a matrix of scatterplots. This allows for simultaneous inspection of bivariate relationships.

col_to_use <- c("Cement", "Slag", "Comp.Strength", "Water", "SLUMP.cm.",
                "FLOW.cm.")
pairs(concrete[, col_to_use], panel = panel.smooth)

pd.plotting.scatter_matrix(concrete[['Cement', 'Slag', 'Comp_Strength', 'Water', 
                                     'SLUMP(cm)', 'FLOW(cm)']], 
                           figsize=(12,12));

We can see that a few of the variables have several 0 values - cement, slag, slump and flow. Water appears to have some relation with slump and with flow.

The scatterplots allow a visual understanding of the patterns, but it is usually also good to compute the correlation of all pairs of variables.

library(psych)
corPlot(cor(concrete[, col_to_use]), cex=0.8, show.legend = FALSE)

corr = concrete[['Cement', 'Slag', 'Comp_Strength', 'Water', 
                 'SLUMP(cm)', 'FLOW(cm)']].corr()
corr.style.background_gradient(cmap='coolwarm_r')
  Cement Slag Comp_Strength Water SLUMP(cm) FLOW(cm)
Cement 1.000000 -0.243553 0.445725 0.221091 0.145913 0.186461
Slag -0.243553 1.000000 -0.331588 -0.026775 -0.284037 -0.327231
Comp_Strength 0.445725 -0.331588 1.000000 -0.254235 -0.223358 -0.124029
Water 0.221091 -0.026775 -0.254235 1.000000 0.466568 0.632026
SLUMP(cm) 0.145913 -0.284037 -0.223358 0.466568 1.000000 0.906135
FLOW(cm) 0.186461 -0.327231 -0.124029 0.632026 0.906135 1.000000

The plots you see above are known as heatmaps. They enable us to pick out groups of variables that are similar to one another. As you can see from the blue block in the lower right corner, Water, SLUMP.cm and FLOW.cm are very similar to one another.

3.6 References

Website References

  1. UCI Machine Learning Repository
  2. Student Performance Dataset.
  3. Kernel density estimation